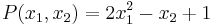Algebraic independence

In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K. This means that for every finite sequence α1, ..., αn of elements of S, no two of which are the same, then if P has coefficients in K and

P(α1,...,αn) = 0

then P is the zero polynomial.

In particular, a one element set {α} is algebraically independent over K if and only if α is transcendental over K. In general, all the elements of an algebraically independent set over K are by necessity transcendental over K, but that is far from being a sufficient condition.

For example, the subset {√π, 2π+1} of the real numbers R is not algebraically independent over the rational numbers Q, since the non-zero polynomial

P(x_1,x_2)=2x^2_1-x_2%2B1

yields zero when √π is substituted for x1 and 2π+1 is substituted for x2.

The Lindemann-Weierstrass theorem can often be used to prove that some sets are algebraically independent over Q. It states that whenever α1,...,αn are algebraic numbers that are linearly independent over Q, then eα1,...,eαn are algebraically independent over Q.

It is not known whether the set {π, e} is algebraically independent over Q.[1] In fact, it is not even known if π+e is irrational.[2] Nesterenko proved in 1996 that:

Given a field extension L/K, we can use Zorn's lemma to show that there always exists a maximal algebraically independent subset of L over K. Further, all the maximal algebraically independent subsets have the same cardinality, known as the transcendence degree of the extension.

References

  1. ^ Patrick Morandi (1996). Field and Galois Theory. Springer. pp. 174. ISBN 978-0-387-94753-2. http://books.google.com/?id=jQ7c8Xqpqk0C. Retrieved 2008-04-11. 
  2. ^ Green, Ben (2008), "III.41 Irrational and Transcendental Numbers", in Gowers, Timothy, The Princeton Companion to Mathematics, Princeton University Press, p. 222 
  3. ^ Nesterenko, Yuri V (1996). "Modular Functions and Transcendence Problems". Comptes rendus de l'Académie des sciences Série 1 322 (10): 909–914. 

See also

External links